Penny sotto la lente: 1st NRG Corp. (FNRC)

1st NRG Corp. è una società di esplorazione e produzione di metano da carbone con sede a Denver, Colorado.

L’attività è incentrata sullo sviluppo di riserve di metano da giacimenti di carbone nel Wyoming, dove opera attraverso una consociata interamente controllata e detiene una partecipazione attiva in 43 pozzi di produzione e 3.018 acri di superficie non ancora sfruttati che potrebbero consentire ulteriori 36 siti, ma dal 2014 la società ha ampliato le proprie attività nell’Ohio, prendendo in gestione un’area di circa 7.000 acri.
La compagnia detiene anche varie partecipazioni in società impegnate in diversi progetti energetici alternativi.

Il titolo, quotato OTC Pink - Nessuna Informazione, è arenato in area 0,0001 $, ma i volumi sono lievitati in modo impressionante di recente.

Penny sotto la lente: eWellness Healthcare Corporation (EWLL)

 

eWellness Healthcare Corporation è un’azienda di “telemedicina” per terapie fisiche con sede in Florida ed attiva dal 2011.

E’ la prima azienda USA ad offrire su larga scala trattamenti monitorati a distanza in tempo reale a pazienti, privati e lavoratori direttamente dall’ufficio. 

Il suo  modello di business prevede infatti che i datori di lavoro possano utilizzare la sua piattaforma di assistenza virtuale per fisioterapisti (PHZIO) quale programma di benessere aziendale completamente monitorato a distanza.
Piattaforma che consente anche l’interconnessione di licenze di terze parti e il monitoraggio del rispetto delle terapie post ricovero da parte di pazienti affetti da diabete, problemi cardiovascolari ecc.

Penny sotto la lente: ICOA - Internet Commerce Of America (ICOA)

 

ICOA Inc. è un’azienda fondata nel 1983  con sede a Warwirk, nel Rhode Island, che fornisce servizi Internet a banda larga sia wireless che cablati negli Stati Uniti. 

Nata come Quintonix e divenuta ICOA nel marzo 1989, essa offre soluzioni di back office per operatori di hotspot e fornitori di servizi wireless fornendo anche servizi di consulenza, oltre a procurare, configurare e installare apparecchiature di rete, attrezzature e ad occuparsi di amministrazione, fatturazione, business intelligence e servizi vari relativi alla gestione dei contenuti. 

Penny sotto la lente: MMEX Resources Corp (MMEX)

MMEX Resources Corp. è una società in fase di sviluppo, figlia di varie acquisizioni e trasformazioni, che si occupa di finanziamento e sviluppo di progetti di esplorazione, estrazione, raffinazione e distribuzione di petrolio, gas naturale, prodotti derivati dal greggio ed energia elettrica (pannelli solari compresi).

Le sue attività sono concentrate su Texas, Perù e altri paesi dell'America Latina e l'obiettivo più significativo del suo piano aziendale è la costruzione di impianti di raffinazione del petrolio greggio nel bacino del Permiano nel Texas occidentale.

Il mercato otc italiano: AIM Italia e il flop del MAC

Le penny stock italiane sono negoziate sul mercato AIM Italia, ma è possibile trovare azioni con valore nominale contenuto anche sul listino principale. Basti pensare, ad esempio, ai tanti bancari quotati sul MTA al di sotto di 2 euro, a Telecom Italia, Juventus FC, RCS Mediagroup, AS Roma etc.

L'AIM, Alternative Investment Market, è un mercato di scambi non regolamentato, regolato e gestito dalla London Stock Exchange (LSE) e per questo non sottoposto alla vigilanza dell’autorità di controllo. 

In fase di ammissione non è infatti richiesta la pubblicazione di un prospetto informativo e successivamente non è richiesta la pubblicazione dei resoconti trimestrali di gestione, ma solo il bilancio e la relazione dell'ultimo semestre.

Penny sotto la lente: Social Life Network (WDLF)

Social Life Network è una piattaforma di social networking aziendale e di consumo basata su blockchain e intelligenza artificiale destinata a settori B2B di nicchia fondata il 1° gennaio 2013 e con sede a Englewood, Colorado.

La società si è quotata il 16 luglio 2016 e il valore nominale delle azioni all’apertura dell’IPO è stato di 50,00 $.

Dagli inizi dell’anno il titolo (mercato Pink - Notizie Attuali) è in caduta libera, stazionandosi in area 0,00010 $, ma notevole l’interesse riaccesosi su di esso in pieno agosto, sia per i diversi accordi raggiunti in ambito e-commerce, sia in ottica di una ripresa dell’economia e di ripartenza delle PMI statunitensi di nicchia.

OTC Markets Group: la galassia over the counter Usa

Le azioni over the counter sono presenti su OTC Markets Group, mercato finanziario con sede a New York che fornisce informazioni su prezzi e liquidità di quasi dodicimila titoli.

Questi sono suddivisi in tre principali mercati: OTCQX, OTCQB e Pink.

Il mercato OTCQX (OTCQX® Best Market) ospita sia multinazionali che ambiscono a vendere le proprie azioni agli investitori statunitensi, sia compagnie nazionali in espansione. Per accedervi esse devono sottoporsi ad una revisione qualitativa da parte di OTC Markets Group e trasmettere a questa le proprie informazioni finanziarie. Non è necessario che si registrino o trasmettano i propri documenti alla SEC.

I mercati over the counter

Over the Counter (OTC) indica il processo con cui un’azione, un titolo in generale, un indice, un derivato o un cross valutario viene scambiato al di fuori di una borsa valori.

L’espressione sembra risalire a quella utilizzata nelle farmacie per i prodotti da banco (“sul bancone”), per i quali non è necessaria la prescrizione medica e i cui prezzi non sono imposti o controllati.
Un mercato OTC ospita dunque negoziazioni che avvengono al di fuori dei circuiti finanziari ufficiali: l’unico principio che determina le quotazioni è l’incontro tra la domanda e l’offerta.

Penny Stock: perché investirci?

Per quello che ci siamo detti sulle penny stock, vale la pena investirci?

In effetti, molti dei fattori di rischio menzionati, quali ad esempio il prezzo molto basso e l’alta volatilità di esso, rappresentano anche elementi che possono tradursi in potenziali vantaggi, poiché il guadagno può essere molto più elevato rispetto a quello che è possibile ottenere da un investimento in titoli di aziende a grossa capitalizzazione e dal valore nominale decisamente più alto.

Le penny stock, inoltre, possono rappresentare strumenti di diversificazione del portafoglio e per strategie di breve periodo, adottando le dovute accortezze che il buon senso richiede.

Senza dimenticare che, al di là delle penny stock OTC, esistono anche penny stock all’interno delle borse più note, come, ad esempio, quella di Milano, il NASDAQ o l’AMEX.

Nulla vieta di iniziare con queste, per le quali è facilissimo recuperare informazioni finanziarie sempre aggiornate, analisi tecniche, segnali di trading e tanti altri strumenti di supporto all’elaborazione delle propria strategia.

Per quanto riguarda le accortezze da adottare per fare un trading consapevole con le penny stock OTC, esse non differiscono da quelle richieste per operare con qualsiasi altro investimento, ma bisogna imporsi ancor maggior rigore nell’elaborare le proprie strategie.

Innanzitutto, quando ci si imbatte in un titolo penny occorre analizzare la società emittente.

Penny Stock: di cosa tener conto prima di prenderle in considerazione

Fatte le dovute premesse, prima di tuffarsi in tale comparto azionario è utile ricordare che:

- le penny stock sono più rischiose delle azioni ordinarie a causa dei prezzi più contenuti e della loro maggiore volatilità. Sono dunque investimenti molto speculativi, che possono rivelarsi anche profittevoli, ma adatti a trader che sono soliti adottare la loro strategia solo dopo un’attenta riflessione sulla compatibilità di uno strumento finanziario con i propri livelli di rischio sostenibile;

- il mercato delle penny stock offre meno liquidità delle borse valori e ciò implica che ogni acquisto o vendita può determinare un forte scostamento dei prezzi. Ma i bassi volumi di negoziazione che si traducono in liquidità contenuta può comportare anche che non si riescano a vendere le azioni detenute nel proprio portafoglio;

- le aziende emittenti penny stock hanno una bassa capitalizzazione di mercato, motivo per il quale le azioni (stock) risultano poco attraenti per i grossi investitori istituzionali e il loro prezzo è molto basso;

- sulle penny stock, abbiamo detto, ci sono poche informazioni disponibili. Diventa dunque complicato assumere decisioni di investimento, ma è complesso anche elaborarne qualcuna. Se l’emittente è obbligato a produrre i documenti contabili ordinari e qualche prospetto finanziario periodicamente alla commissione di vigilanza dei mercati del paese di appartenenza o di quello dove sono negoziate le sue azioni, è comunque difficilissimo recuperare relazioni e analisi tecniche e spesso gran parte di quelle disponibili sono diffuse da fonti poco attendibili;

Penny Stock: cosa sono e come funzionano (parte 2°)

 

Introducendo le penny stock ho accennato ai mercati over the counter: non deve trarre in inganno, tuttavia, l’utilizzo dell’espressione “mercati non regolamentati”.
Se tendenzialmente le penny stock non quotate su una borsa valori sono molto più rischiose delle altre, anche i mercati over the counter (OTC) sono soggetti a vigilanza, per quanto più contenuta.

Sono soprattutto OTC, inoltre, i due mercati più liquidi al mondo, vale il mercato dei cambi (oltre il 75% del Forex viene negoziato over the counter) e quello dei derivati (la parte di questo che transita sulle piazze regolamentate è minima). 

Si tratta di due mercati dove ogni giorno transitano volumi pari a quasi venti volte il Pil mondiale, capaci di generare una liquidità tale da mantenere in piedi il sistema finanziario anche nei periodi più bui dell’economia globale.

Penny Stock: cosa sono e come funzionano

 

Misterioso oggetto del desiderio sia per investitori alle prime armi che per quelli che hanno già una discreta conoscenza del mondo degli investimenti ed esperienza nel trading, solo o esclusivamente un grande bluff per tanti altri, le penny stock rappresentano, relativamente, una grande novità nel panorama italiano, una tipologia di investimento rischioso e spesso molto speculativo, dove i rischi di trading sembrano più elevati del solito. E non solo per le strategie di “pompaggio” cui ho accennato nella prefazione di Penny Stock: il trading (im)possibile disponibile qui e ben rappresentate nel noto film di Scorsese con protagonista DiCaprio nei panni del “Lupo di Wall Street”.

Ma cosa sono le penny stock?

Debito e governo tecnico: c'è una patrimoniale dietro l'angolo?

Nella rilevazione di Bankitalia relativa al mese di febbraio 2020 il debito pubblico italiano ha fatto registrare ancora una crescita, toccando quota 2.447 miliardi di euro rispetto ai circa 2.444 miliardi del mese precedente.
A fine 2019 il debito pubblico italiano era pari a poco meno di 2.409 miliardi, 38 miliardi in più rispetto al dato rilevato al 31 dicembre 2018 (2.381 miliardi) ma comunque lontano dal massimo storico registrato a luglio 2019 (2.467 miliardi).

In termini di rapporto debito/PIL siamo intorno al 140% e la situazione attuale e nell’immediato futuro, con la pandemia di covid-19 in corso, non può che tragicamente peggiorare, bruciando anche l’effetto positivo dovuto al calo degli interessi che si sta registrando, più o meno costantemente, dal 2015.

E a proposito di interessi sul debito, lo scorso anno questi hanno raggiunto il 3,4% del PIL (dal 3,7% dell’anno precedente), mentre l’avanzo primario l’1,7% (dall'1,5%): una crescita evidentemente insufficiente anche a coprire i soli interessi.
Scenario, quest’ultimo, già da solo in grado di evidenziare quanto possa essere praticamente impossibile in futuro generare ricchezza aggiuntiva per abbattere il debito pubblico (che non è altro che l’anticipo di redditi futuri) attraverso la tassazione.

Da un paio di anni, inoltre, qualche ex ministro e leader di partito, in passato erettosi a strenuo difensore del risparmio degli italiani, parla di interventi straordinari per cercare di riportare il debito pubblico a livelli più adeguati tirando in ballo una possibile patrimoniale, magari ridefinendola con un nome diverso.

Di fatto ci sono circa 1.500 miliardi di euro parcheggiati sui conti correnti dagli italiani ed è un tesoretto che potrebbe ingolosire molti.
Il mondo della politica ha finora escluso tale scenario, ma spesso il lavoro sporco lo si fa fare ad un tecnico, magari che goda anche di una certa autorevolezza in campo internazionale.
Sfumata lo scorso agosto tale prospettiva, sarà l’emergenza covid-19 a dare il la ad un governo di tecnici e ad un provvedimento di questo tipo?

Emergenza coronavirus: già 3,4 milioni le famiglie italiane che hanno perso più della metà delle entrate. Oltre un milione quelle a reddito zero

L’emergenza coronavirus ha costretto milioni di italiani a blindarsi in casa e le ripercussioni, già drammatiche sul piano sociale, non si sono fatte attendere anche dal punto di vista economico.
Da un’indagine condotta da mUp Research e Norsta per conto di Facile.it su un campione di quasi 18,5 milioni di famiglie italiane, 10.800.000 (il 58,6%) ha dichiarato di aver registrato un calo del proprio reddito.

Di esse, nello specifico, il 12,1% (più di 2.200.000) ha dichiarato di aver perso più del 50% del reddito familiare e il 6,4% di aver visto svanire la totalità delle entrate.
Stiamo parlando, quindi, di 3,4 milioni di famiglie che hanno visto più che dimezzare le proprie entrate, con quasi 1.180.000 precipitate in una condizione di “reddito zero”.

Dal punto di vista territoriale il calo dei redditi ha interessato l’Italia tutta, con picchi al Sud e nelle isole.
Qui la perdita totale di entrate ha riguardato il 7,5% degli intervistati, mentre ammonta al 12,7% la percentuale di coloro che hanno visto i loro introiti più che dimezzarsi.

Il dibattito che non c'è

Lunghetto ma interessante

https://youtu.be/mvDrRYvqBfo

Fondo salva-Stati: MES e coronavirus, la soluzione che non accontenta nessuno

Il dibattito sul MES non conosce tregua e, dopo due anni di incontri-scontri in ambito UE, anche il coronavirus diventa motivo di battaglia su questo fondo salva-Stati.
D’altronde potrebbe essere uno degli strumenti da impiegare per fronteggiare l’emergenza sanitaria (e sociale) legata alla diffusione del covid-19, ma per ora, come per gli Eurobond, sembra di assistere soltanto a soluzioni accennate o parziali.

Intanto la vera svolta finora è stata la Bce che, tra questo mese e dicembre, acquisterà un quantitativo addizionale di titoli di Stato pari al 4,5% del Pil.
La Banca centrale europea, come stabilito dal Trattato Ue, non può infatti finanziare direttamente i Paesi membri, ma può acquistare i titoli di Stato sul mercato secondario.
Ciò implica che per poter ottenere il sostegno dei programmi della Bce messi in piedi per fronteggiare la recessione da pandemia covid-19 i singoli Stati devono accedere al mercato emettendo titoli pubblici.
Gli acquisti della Bce stanno consentendo ai Paesi più indebitati di finanziare la loro economia in deficit senza vedere schizzare gli spread, ma occorre ben altro per fronteggiare la situazione attuale e spingere per una ripresa futura.

Fondo salva-Stati: chi sono i veri nemici del MES e quali le critiche principali

Argomento dibattuto da tanto e ritornato veementemente al centro della cronaca proprio in piena pandemia coronavirus, il MES e la sua riforma sembrano ormai occupare molto più spazio di quanto ci si sarebbe immaginato, soprattutto per la specificità della materie e la necessaria razionalizzazione dei fondi europei istituiti per allontanare lo spettro default e il rischio contagio nell’eurozona.

Le polemiche sul tema hanno assunto toni a tratti anche aspri e spesso fuorvianti, quasi a capovolgere gli originari assi pro e contro il fondo salva-Stati messo in campo in piena recessione mondiale nel 2012, durante la fase più cruenta della crisi dei debiti sovrani.

Chi l’ha voluta e votata senza battere ciglio oggi si erge infatti a baluardo dei detrattori della stessa e fiero oppositore dell’UE tutta, come sovente accade in questi anni dove, complice la difficoltà dei cittadini a storicizzare gli eventi e il sopravvento delle urla e della narrazione sulla realtà, chi ha adottato dei provvedimenti li demonizza quando non è più alla guida delle istitutzioni, mentre chi all’epoca era all’opposizione e magari ha sollevato anche qualche critica si ritrova a gestirne poi le conseguenze diventandone il più strenuo difensore.

Al di là di questo trend di fondo che inquina non poco la comprensione degli eventi e dei fenomeni, quali sono i Paesi avversi fin dalle origini al MES e le criticità principali sollevate dagli stessi?

Gli Stati membri dell’Unione che non accettano il Meccanismo Europeo di Stabilità come istituito fin dalle origine sono quelli del Nord Europa.

Fondo salva-Stati: cosa cambierebbe con la riforma MES

La riforma del Meccanismo Europeo di Stabilità sta andando avanti da un paio di anni e non si è riusciti a chiuderla entro dicembre come da calendario dei lavori.

Già ai principi del 2018 l’Eurogruppo iniziò a proporre di utilizzare il MES, adoperato durante la crisi dei debiti sovrani per calmierare la speculazione sulla Grecia e gli altri membri Ue che all’epoca hanno fatto richiesta di aiuti all’Unione, come fondo europeo unico da impiegare non soltanto nelle emergenze di rischio default ma anche come paracadute finale del fondo di risoluzione unico della banche (RSF), dotandolo così di nuove funzioni e nuovi poteri.
Con questa nuova funzione di backstock esso verrebbe dotato di una linea di credito da 70 miliardi alla quale gli Stati potranno accedere qualora i loro fondi nazionali per le risoluzioni bancarie, costituiti con le risorse delle banche e non con fondi pubblici, non risultino sufficienti a scongiurare una crisi del sistema creditizio e a garantire investitori e risparmiatori.

Un'altra novità riguarda l'introduzione di linee di credito precauzionali (molto più serie di quelle attuali in termini quantitativi) adoperabili nel caso la salute finanziaria di uno Stato membro venga messa a dura prova da uno shock economico ed esso voglia scongiurare il rischio fondato di precipitare nella morsa della speculazione sui mercati finanziari.

Valutazione degli investimenti finanziari

Uno degli oneri in capo al consulente finanziario è quello di valutare se il grado di rischio e di rendimento di un investimento è coerente con il profilo e le esigenze del cliente.

Sono perciò messi a sua disposizione tutta una serie di strumenti per la valutazione degli investimenti, dagli indicatori sintetici pubblicati dalla stampa economica specializzata ai report resi disponibili dagli uffici studi delle Sim per cui opera, per il cui corretto utilizzo è necessario conoscere alcuni concetti di base.

1. Tasso Interno di Rendimento (IRR)

Il tasso interno di rendimento (internal rate of return - IRR) è quel tasso d’interesse che eguaglia la somma dei valori attuali dei pagamenti distribuiti in più periodi al valore (corrente) dell’attività da cui sono generati.
L’individuazione analitica dell’IRR non è agevole e, di conseguenza, si ricorre spesso all’uso di approssimazioni successive per ottenere una soluzione attraverso un processo lineare.
Dal punto di vista formale, l’equazione che consente di individuare il tasso interno di rendimento è:

dove:

• Aₜ è il saldo tra entrate e uscite al tempo t

• n è l’ultimo periodo in cui vi è un’entrata o un uscita.

2. Valutazione dei titoli a reddito fisso.

I titoli a reddito fisso sono quelli che garantiscono una data somma di denaro in quanto rappresentano un rapporto obbligatorio (di credito) tra emittenti e investitori.

I titoli obbligazionari (strumenti di mercato monetario, titoli di Stato e obbligazioni emesse da organismi privati) forniscono reddito in tre distinte forme:

• cedole periodiche;

• perdite o guadagni in conto capitale;

• interessi derivanti dal reinvestimento delle cedole.

2.1 Titoli zero coupon

Sono i titoli che non pagano cedole e che, dunque, prevedono un unico flusso di rimborso a scadenza (BoT e CTz, ad esempio).
La determinazione del rendimento di un titolo zero coupon può essere basata sul regime di capitalizzazione semplice o composta. 

• Rendimento semplice

dove con gg si indicano i giorni mancanti alla scadenza.

• Rendimento composto

2.2 Titoli con cedola

Per quanto esistano emissioni a tasso indicizzato, per la valutazione di un titolo con cedole si considera, di solito, un titolo obbligazionario il cui tasso d’interesse si assume essere fisso e che può essere emesso alla pari (ad un prezzo coincidente con il suo valore nominale), sopra la pari o, caso più frequente, sotto la pari.
I tre indicatori più utilizzati sono:

• Tasso di Rendimento Nominale (TRN)

Il tasso di rendimento nominale (o “facciale”) di un titolo a reddito fisso con cedole è calcolato sulla base del valore nominale del titolo (VN), come rapporto tra il valore delle cedole corrisposte in un anno (CE) ed esso:

Non tenendo conto della differenza tra il prezzo nominale e quello realmente pagato per l’acquisto, delle frequenze con cui vengono pagate le cedole e della vita residua del titolo, il TRN risulta un indicatore poco significativo.

• Tasso di Rendimento Immediato (TRI)

Il TRI è il rapporto tra il valore delle cedole corrisposte in un anno e il valore capitale del titolo (al corso secco):

E’ più significativo del TRN poiché considera il prezzo d’emissione dell’obbligazione, ma trascura anch’esso la frequenza con cui vengono pagate le cedole e la vita residua del titolo.

• Tasso di Rendimento Effettivo a Scadenza (TRES)

Il tasso di rendimento effettivo a scadenza (TRES o YTM - Yield To Maturity) consente di valutare la profittabilità di un titolo basandosi sul corso tel quel, sui flussi di capitale dati dalle cedole e sul loro ammontare, sulle condizioni di rimborso del capitale e su ogni altro fattore che possa influenzare il valore attuale dell’obbligazione.

Viene calcolato seguendo la stessa logica del tasso interno di rendimento sulla base della seguente formula:

dove:

VA rappresenta il valore attuale del titolo (ossia il corso tel quel),
T la scadenza,
F i flussi periodici che vengono corrisposti al possessore.

Il corso tel quel tiene in considerazione, oltre al valore capitale, anche la ratio degli interessi maturati fino a quel periodo, considerando quindi, in ogni momento, il prezzo d’acquisto del titolo.

Il presenza di titoli con cedola, il corso secco e il tel quel coincidono al momento della scadenza della cedola (o meglio, appena essa è scaduta), mentre negli altri casi, di norma, il corso tel quel supera il corso secco.

corso tel quel = corso secco + rateo di cedola (quota già maturata).

Nel caso di titolo sprovvisto di cedola (privata prima della scadenza) si parla invece di corso ex cedola.

corso ex cedola = corso tel quel - cedola = corso secco - rateo interessi futuri.

I limiti del TRES risiedono nelle ipotesi alla base di esso, vale a dire:

• tasso di reinvestimento dei flussi (cedole) al TRES stesso;

• detenzione dei titoli fino alla scadenza.

(continua)

Appunti di matematica finanziaria per la valutazione degli investimenti (parte 2)

Tra i concetti di matematica finanziaria da conoscere per valutare gli investimenti non possono mancare la rendita e l'ammortamento.
Impossibile per un analista, un consulente finanziario, un trader o chiunque si occupi di finanza, titoli, polizze e finanziamenti ignorarli.

1. Rendita

Per rendita si intende un insieme di prestazioni finanziarie, consecutive e scaglionate nel tempo.
Si tratta, dunque, di un flusso finanziario protratto nel tempo, la cui singola prestazione è definita “rata della rendita” (si pensi, ad esempio, al rimborso di un prestito, un leasing, un mutuo o un’obbligazione).

Le tipologie di rendite oggetto di studio sono:

• Rendite certe
  
  

Sono le rendite per le quali le rate sono fissate a priori nella quantità, nell’ammontare e nelle epoche.

• Rendite aleatorie

Sono quelle rendite, tipiche delle attività assicurative, per le quali le prestazioni finanziarie sono condizionate dal verificarsi di un determinato evento.

• Rendite periodiche

Sono tutte quelle per cui l’intervallo temporale tra le rate successive è costante.

• Rendite aperiodiche

Sono tutte quelle per cui la cadenza temporale è opposta alla precedente.

• Rendite anticipate

Per esse il pagamento delle rate avviene all’inizio del periodo di riferimento.

• Rendite posticipate

Con esse il pagamento delle rate avviene alla fine del periodo di riferimento.

• Rendite temporanee

Il riferimento è a quelle per cui il numero delle rate è finito.

• Rendite perpetue

Si tratta del caso esattamente opposto al precedente, dove il numero delle rate è infinito.

• Rendite costanti

Per esse le rate sono di uguale ammontare.

• Rendite variabili

Caso opposto al precedente, dove le rate sono di diverso ammontare (si pensi, ad esempio, alle rendite indicizzate ad un parametro).

Valutazione di una rendita

Valutare una rendita significa quantificare, in un dato momento, il valore totale dei flussi a cui essa dà diritto. In genere, per la valutazione si sceglie come istante di riferimento il momento iniziale o quello finale di pagamento delle rate: nel primo caso, si ha il valore attuale della rendita, vale a dire la somma di tutti i valori attuali di tutte le rate, nel secondo il montante della rendita, la somma dei montanti. In tali casi si parla di rendita immediata.

Nel caso in cui la valutazione del valore attuale venga fatta in un momento precedente all’inizio della corresponsione delle rate si parla invece di rendita differita.

• Valori di rendite in un orizzonte temporale determinato 

Considerando il caso in cui le rate vengono distribuite per un numero finito di anni n, in un regime di costanza intertemporale dei tassi d’interesse (curva dei tassi piatta), il valore attuale di una rendita è uguale alla sommatoria dei flussi finanziari che la compongono (attualizzati).
Dato i il tasso di attualizzazione, la formula è la seguente:

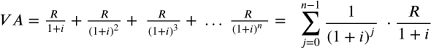
che può essere riscritta come:

Essa rappresenta il valore attuale di una rendita posticipata immediata di rata R, n anni, al tasso i, in regime di interesse composto.

Nel caso in cui la rendita sia differita di t anni, il valore attuale è:

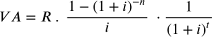
Per calcolare il valore attuale di una rendita anticipata occorre moltiplicare la formula per il fattore (1+i).

Per quanto riguarda il calcolo del montante di una rendita, allo sconto si sostituisce la capitalizzazione dei flussi di cassa e la formula diventa:

che può essere riscritta come:

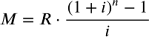
L’equazione esprime il montante di una rendita annua posticipata immediata di rata R, di anni n, al tasso i.
Nel caso la rendita fosse anticipata, per calcolare il montante è sufficiente moltiplicare la formula per il fattore (1+i).

• Valori di rendite in un orizzonte temporale indeterminato

Nel caso in cui l’orizzonte temporale sia indeterminato, il valore attuale di una rendita posticipata immediata è:

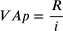
e, noto il valore attuale di VAp e le relative rate costanti, il tasso di rendimento è dato da:

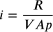
Nel caso di una rendita perpetua anticipata immediata, la formula diventa:

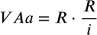
da cui, noto VAa:

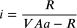
2. Ammortamento dei prestiti

• Ammortamento a rata costante

Si tratta di un piano di rimborso, detto anche ammortamento alla francese, che prevede che le annualità, o rate, corrisposte posticipatamente siano tutte dello stesso ammontare.
Il valore della rata si calcola utilizzando la formula vista per il calcolo del valore attuale di una rendita:

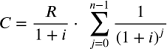
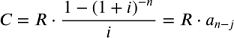
da cui:   

 

Alla fine del t-esimo periodo il debito residuo è:

Dato il tasso di sconto :

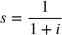
il valore della quota capitale al periodo n è:

da cui:

Vista la costanza di R, i pagamenti di un anno devono essere uguali a quelli dell’anno precedente, dunque:

da cui:

,

• Ammortamento a rata decrescente

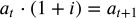Si tratta di una metodologia di rimborso, detto ammortamento all’italiana, che prevede la costanza della quote capitali mentre le quote di interesse sono decrescenti.